La somme de deux vecteurs de référencement
La propriété de la somme vectorielle appliquée ici à la thématique des liens va permettre de nous montrer l’importance de deux éléments qui sont la puissance ou la notoriété de page (module du vecteur) et la thématique (argument du vecteur)
La somme vectorielle pour expliquer l’intérêt de référencer dans la bonne thématique.
La situation est simple, nous allons vectoriser chaque backlink de la façon suivante : le module du vecteur est donné par la puissance ou l’autorité de la page sur laquelle on est et l’argument du vecteur par la thématique de la page sur laquelle on est. On imagine que l’on fabrique des liens vers une page donnée dont la thématique est le référencement.
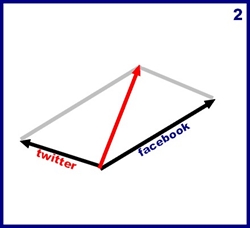
Sur le graphique 1 les deux arguments sont assez proches l’un de l’autre on peut donc imaginer que l’on a fait un lien dans twitter sur une thématique comme google par exemple et sur facebook dans un thème comme le référencement. Les arguments étant proches le vecteur résultant à un grand module. Situation très intéressante.
Sur le graphique 3 les arguments sont les mêmes mais la page facebook sur laquelle on a mis le lien est un groupe avec peu de membres et donc un module de vecteur nettement moindre que sur le graphique 1. Le vecteur résultant a donc un module plus petit et le référencement sera moins impacté par la somme de ces deux liens.
La situation est simple, nous allons vectoriser chaque backlink de la façon suivante : le module du vecteur est donné par la puissance ou l’autorité de la page sur laquelle on est et l’argument du vecteur par la thématique de la page sur laquelle on est. On imagine que l’on fabrique des liens vers une page donnée dont la thématique est le référencement.
Sur le graphique 1 les deux arguments sont assez proches l’un de l’autre on peut donc imaginer que l’on a fait un lien dans twitter sur une thématique comme google par exemple et sur facebook dans un thème comme le référencement. Les arguments étant proches le vecteur résultant à un grand module. Situation très intéressante.
Sur le graphique 3 les arguments sont les mêmes mais la page facebook sur laquelle on a mis le lien est un groupe avec peu de membres et donc un module de vecteur nettement moindre que sur le graphique 1. Le vecteur résultant a donc un module plus petit et le référencement sera moins impacté par la somme de ces deux liens.
Si les deux thèmes sont exactement les mêmes donnant des vecteurs alignés la somme est idéale mais il n’est pas toujours possible de trouver le même objet quand on pose des liens vers une page donnée dont la thèmatique est très précise et parfaitement définie.
Ce même si les arguments sont opposés (-pi et pi par exemple) on imagine que l’on perd totalement l’efficacité de la situation (vecteur nul !)
Ce même si les arguments sont opposés (-pi et pi par exemple) on imagine que l’on perd totalement l’efficacité de la situation (vecteur nul !)