Produit de deux matrices pour calculer l’autorité d’une page
On sait que Matt Cutt a annoncé qu’il voulait diminuer un peu l’importance de la notoriété d’une page au niveau du calcul de sont autorité ce qui veut réellement dire sont empreinte sur les résultats dans les moteurs de recherche
Shéma du produit matriciel de base
Une idée pour introduire le produit de deux matrices dans un cours de maths.
Mise en situation : on sait que Matt Cutts a fait part de sa volonté de donner moins d’importance à la notoriété d’un site dans le calcul de son autorité. On se doit donc d’imaginer que les calculs au niveau de l’algorithme vont être différents. Mais on se dit aussi que tout doit être parfaitement prévu de la part des ingénieurs Google et qu’il n’y aura qu’un seul coefficient à changer pour que l’autorité soit modifiée et donc les résultats dans les moteurs de recherche directement impactés.
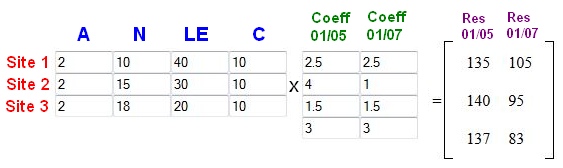
Partons donc d’une situation volontairement simplifiée qui permet de calculer l’autorité de trois sites différents. Les critéres utilisés pour ce calcul sont l’ancienneté (A), la notoriété (N), les liens entrants (LE) et la qualité du contenu du site (C)
Exemple avec un site qui a une belle ancienneté (A) : les tables de billards de grand dépôt à la Roche de Glun (26600)
Pour simplifier aussi j’ai choisis des sites avec un contenu de valeur (10 pour chacun) et une ancienneté de 2 ans pour tous. La différence d’autorité se fait donc sur la notoriété (j’aime de google, nombre de tweet, nombre d’abonnés, nombre de visites etc.) et les liens entrants.
Notons qu’avec le coefficient de 4 pour la notoriété c’est le site 2 avec une autorité résultante de 140 qui est devant au 01/05.
Mais en passant ce coefficient à 1 on a de suite un changement d’ordre et le site 1 qui était dernier au 01/05 devient premier au 01/07.
Ce petit exemple qui n’est que pure fiction au point de vu des algorithmes de google permet de donner de l’intérêt à cette opération sur les matrices et montre bien que ce produit permet de changer facilement un classement par le changement d’un seul coefficient